Pembuktian Teorema Binomial dengan Induksi Matematika
 Sebelum kita membuktikan teorema binomial, kita akan membahas rumus yang akan digunakan untuk membuktikan teorema binomial tersebut, yaitu rumus Pascal. Rumus Pascal, yang dinamai oleh matematikawan dan ahli filsafat asal Prancis Blaise Pascal, merupakan satu dari beberapa rumus yang sangat terkenal dan berguna pada kajian masalah pencacahan. Rumus Pascal menghubungkan nilai kombinasi r dari n + 1 objek dengan kombinasi r – 1 dan r dari n objek. Secara lebih jelas, rumus Pascal menyatakan bahwa,
Sebelum kita membuktikan teorema binomial, kita akan membahas rumus yang akan digunakan untuk membuktikan teorema binomial tersebut, yaitu rumus Pascal. Rumus Pascal, yang dinamai oleh matematikawan dan ahli filsafat asal Prancis Blaise Pascal, merupakan satu dari beberapa rumus yang sangat terkenal dan berguna pada kajian masalah pencacahan. Rumus Pascal menghubungkan nilai kombinasi r dari n + 1 objek dengan kombinasi r – 1 dan r dari n objek. Secara lebih jelas, rumus Pascal menyatakan bahwa,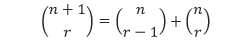
dengan n dan r adalah bilangan bulat positif dan r ≤ n. Rumus ini dapat digunakan untuk mempermudah penghitungan nilai kombinasi yang besar dengan menuliskannya ke dalam kombinasi yang lebih kecil: Jika nilai kombinasi r dari n objek diketahui, maka nilai kombinasi r dari n + 1 objek dapat dihitung untuk semua r sedemikian sehingga 0 < r ≤ n.
Segitiga Pascal, seperti yang ditunjukkan oleh gambar di bawah ini, merupakan versi geometris dari rumus Pascal.
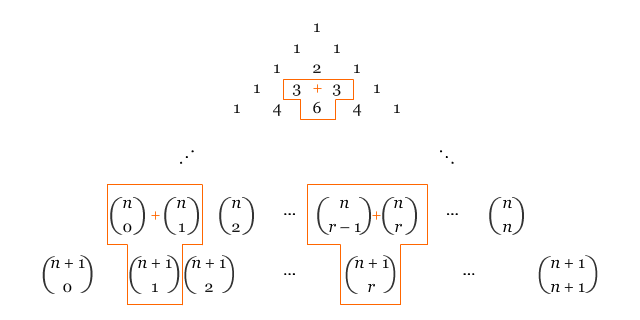
Setiap bilangan pada segitiga di atas sama dengan kombinasi r dari n objek. Rumus Pascal menyatakan bahwa bilangan pada baris r dan kolom n + 1 sama dengan bilangan pada baris n kolom r – 1 ditambah dengan bilangan pada baris n kolom r. Hal ini berarti, bilangan yang ada di dalam segitiga Pascal sama dengan penjumlahan dari dua bilangan yang terletak tepat di sebelah kiri-atas dan kanan-atasnya. Selanjutnya, bagaimana kita membuktikan rumus Pascal tersebut? Berikut ini pembuktian rumus Pascal dengan pendekatan kombinasi.
Bukti Misalkan n dan r adalah bilangan bulat positif dengan r ≤ n dan S adalah himpunan yang memiliki n + 1 anggota, atau S = (x1, x2, x3, … , xn + 1}. Sehingga, himpunanS sama dengan gabungan dari {x1, x2, x3, … , xn} dan {xn + 1}. Selanjutnya, semua himpunan bagian dari S yang bilangan kardinalnya sama dengan r dapat dibagi menjadi dua kelompok: kelompok pertama merupakan himpunan bagian yang memuat xn + 1, dan kelompok yang lain merupakan himpunan bagian yang tidak memuat xn + 1.
Apabila suatu himpunan bagian dari S memuat xn – 1, maka himpunan bagian tersebut akan memuat r – 1 anggota dari {x1, x2, x3, … , xn}. Jika himpunan bagian dari S tidak memuat xn – 1, maka himpunan bagian tersebut akan memuat r anggota dari {x1, x2, x3, … ,xn}.
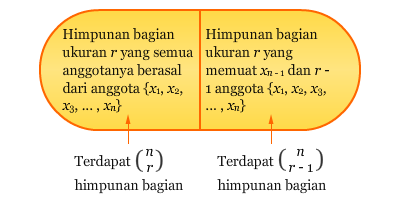
Karena banyaknya himpunan bagian S yang berukuran r sama dengan kombinasi r dari n+ 1, maka
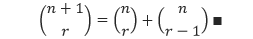
Pembuktian Teorema Binomial dengan Induksi Matematika
Misalkan a dan b adalah sembarang bilangan real, dan P(n) adalah pernyataan
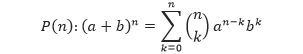
Tunjukkan bahwa P(0) benar: Untuk n = 0, teorema binomial menyatakan bahwa:
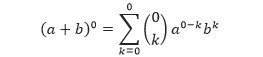
Tetapi ruas kirinya adalah (a + b)0 = 1, dan ruas kanannya adalah
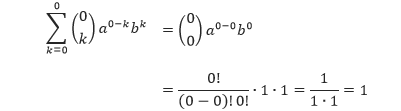
Sehingga P(0) benar.
Tunjukkan bahwa untuk setiap bilangan bulat m ≥ 0, jika P(m) benar, makaP(m + 1) benar: Misalkan diberikan m bilangan bulat dengan m ≥ 0 dan P(m) benar. Sehingga,
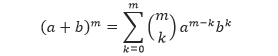
Selanjutnya, kita akan menunjukkan bahwa P(m + 1) benar:
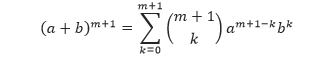
Sekarang, berdasarkan definisi pangkat (m + 1),
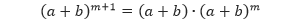
Sehingga dengan substitusi dari hipotesis induktif,
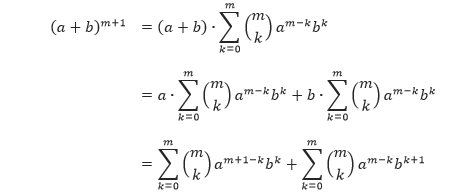
Selanjutnya, kita transformasikan penjumlahan kedua pada ruas kanan di atas dengan mengubah variabel j = k + 1. Ketika k = 0, maka j = 1. Ketika k = m, maka j = m + 1. Karenak = j – 1, maka
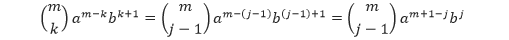
Sehingga, penjumlahan kedua pada ruas kanan tersebut akan sama dengan,
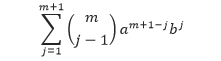
Karena dalam penjumlahan tersebut j adalah variabel semu, maka kita dapat mengubah jmenjadi k asalkan pengubahan tersebut untuk semua j yang muncul dalam penjumlahan tersebut.
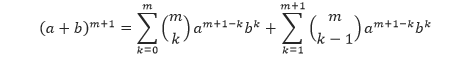
Sehingga,
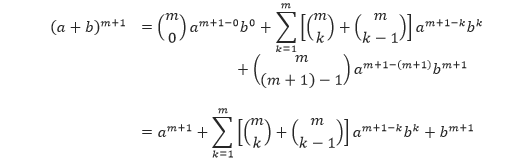
Berdasarkan rumus Pascal,
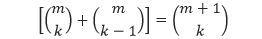
Sehingga,
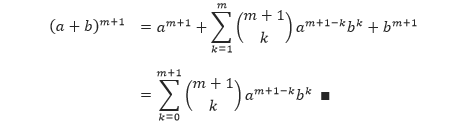
Semoga bermanfaat,
Tidak ada komentar:
Posting Komentar